교류의 표현 1 - 순시값, 실효값, 평균값
발전기의 전기를 만드는 회전자가 1회전할 때(한 바퀴 돌 때) 시간(x축)에 따라 나오는 출력을 아래 그림으로 표시하였다
이를 정현파(sine wave) 교류라 부르며, 표현 방법에 따라 각각 순시값, 실효값, 평균값으로 다양하게 나타냅니다
y축을 전압, x축을 시간으로 표현한 그림이지만, 전류에 대해서도 같은 모습이 나옵니다
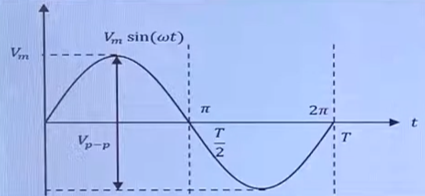
먼저 순시값 (매 순간의 시간에 따른 값)에 대해 알아보겠습니다
위 그림을 보면 전압 v가 시간 t가 흘러가면서 계속 변하고 있음을 알 수 있습니다
교류는 직류와 달리 전압, 전류 등을 소문자로 표현하고,
전압 v 및 전류 i의 시간 t에 따른 변화는 아래와 같이 표현하며, v(t) 및 i(t)를 전압, 전류의 순시값이라고 부릅니다
v(t) = Vm sin( ωt ± θv ) [V]
i(t) = Im sin( ωt ± θi ) [A]
Vm : 전압의 최대값, Im : 전류의 최대값,
ω : 각속도라 부르며 ω = 2πf [rad/sec]
θ : 위상각이며 (+)일 때 앞선다, (-)일 때 뒤진다고 표현하며 이 개념은 교류의표현-9에서 다루도록 하겠습니다
참조1, 라디안 개념에 대해 살펴보면 다음과 같습니다

각속도(각주파수) ω는 각도 변화 θ를 시간 t로 나눈 것으로 (단위 시간당 변하는 각도를 각속도로 표시)
ω = θ / t = 2π / T = 2πf
위 식에서 한 바퀴의 각 2π (360도)를 주기 T(한 바퀴 도는데 걸리는 시간)로 나눈 것과 진동수 f(초당 회전수)로 곱한 것은
예를 들어, 한 바퀴 도는데 걸리는 시간이 5초라고 할 때
ω = 2π / T = 2π / 5 = 0.4π / sec
= 2π f = 2π x 1/5 = 0.4π / sec
똑 같습니다
참조2. 주기 T와 주파수 f의 관계를 다시 살펴보면
T = 1 / f
파동이 한 번 진동하는데 걸리는 시간을 주기 T라고 정의하면
한 번 진동하는데 3초가 걸렸다면 주기 T = 3 sec가 된다
파동이 1초 동안에 몇 번 진동하는지를 주파수 또는 진동수 f (frequency)라고 정의하면
주파수의 단위는 헤르쯔 (Hz = 1/sec)로 표시하는데
1초에 50번 진동한다면 진동수 f = 50 Hz = 50 / sec가 된다
맨 위 그림을 예로 순시그래프를 통해 T와 f를 다시 살펴보면,
시간이 지나감에 따라 v는 위로 아래로 볼록하며 다시 아래로 볼록 변하고,
주기 T가 10초라고 할 때, 10초만에 2π 라디안의 각도를 움직인 것이며
위로 아래로 볼록이 각각 1 개, v=0인 점이 시작점 포함하여 세 번 온다.
여기서 f는 얼마일까? 주기 T의 역수이므로 1 / 10 = 0.1 / sec가 된다 (1초에 0.1바퀴 돌아간다는 뜻)

참조3. 각속도에 대해 조금 더 심화된 이해를 해 봅시다
각속도 ω는 시간 t당 움직인 각도 θ이므로
ω = θ / t [각도/시간]
이며, 이는 단위시간당(보통은 1초) 몇 도의 각도가 움직이는지 나타내는 각의 속도가 됩니다
그렇다면 시간이 지남에 따라 이동한 거리, 여기서는 이동한 각도 θ는
θ = ωt
가 됩니다
예를 들어, 각속도가 ω = 180도 (1/2바퀴)/초 혹은 단위를 바꾸어서 ω = π 라디안/초 라고 하면,
2초 후 지나친 각도는 (일반적인 속도를 말하면, 2초 후의 거리)
θ = ωt 이므로
θ = 180도/초 x 2초 = 360 도
θ = π라디안/초 x 2초 = 2π 라디안
으로 한 바퀴를 돈 것이 됩니다
참조4. 그렇다면 순시값에 있는 v(t) = Vm sin( ωt ± θ ) 식은 어떻게 나타나게 되었을까요?
1) 아래 좌측 그림처럼 x,y 좌표계에서 반지름이 1이고 원점이 (x,y)=(0,0)인 단위원에서 (1,0)인 빨간 점을 반시계 방향으로 각도 θ만큼 움직입니다
2) 빨간 점이 움직일 때, 움직이는 각도에 따른 sin(θ) = 높이/빗변 값을 찾아서 각도에 따라 점을 찍어 보면
아래 우측 그림처럼 각도가 변화함에 따라(x축) θ의 함수인 sin(θ)값을 y축에 그릴 수 있습니다
이렇게 각도에 따른 사인파(sine wave, 정현파) 곡선의 식은 아래와 같이 표현됩니다 (a = 1)
y = f(θ) = a sin θ

y = f(θ) = sin(θ) 는
θ가 0도 일때 0
θ가 90도(π/2) 일때 1..
이렇게 빨간 점이 움직인다는 의미입니다
ω = θ / t --이므로--> θ = ωt 이므로
각도 θ의 함수인 식을 시간 t의 함수로 아래와 같이 바꿀 수 있습니다
f(θ) = a sin θ
f(t) = a sin (ωt)
순시값 v(t) = Vm sin( ωt ± θ ) 식을 살펴보면,
f(t) = a sin (ωt) 식에서
a가 Vm으로 바뀌어 사용된 것이고 (진폭이 1이 아닌 값임을 의미)
sin (ωt)는 같으며
θ는 본질을 교란시키는 부가적 요인이므로, 제외하고 생각하면
결국 같은 형태임을 알 수 있습니다